TOPIC INFO (UGC NET)
TOPIC INFO – UGC NET (Geography)
SUB-TOPIC INFO – Geographical Techniques (UNIT 9)
CONTENT TYPE – Detailed Notes
What’s Inside the Chapter? (After Subscription)
1. Introduction
2. Geodesy
3. Earth Models
4. Ellipsoid Models
5. Use of Geoid, Sphere and Ellipsoid
6. Which is the Best Reference Ellipsoid for You?
7. Concept of Datum
7.1. Horizontal Datum
7.2. Vertical Datum
8. Coordinate System
8.1. Geographic Coordinate System
8.2. Planar Coordinate System
9. Map Projections
9.1. Construction of Map Projection
9.2. Scale Factor and Transformation
10. Classification of Map Projections
10.1. Nature of Projection Surface
10.2. Coincidence of Projection Surface
10.3. Position of the Projection Surface
10.4. Properties of Projection
11. False Origin of Projection
12. Commonly Used Map Projections
12.1. Mercator Projection
12.2. Transverse Mercator (TM) Projection
12.3. Universal Transverse Mercator (UTM) Projection
12.4. Lambert Conformal Conic (LCC) Projection
12.5. Polyconic (PC) Projection
13. Choosing Suitable Map Projection
Note: The First Topic of Unit 1 is Free.
Access This Topic With Any Subscription Below:
- UGC NET Geography
- UGC NET Geography + Book Notes
Georeferencing
UGC NET GEOGRAPHY
Geographical Techniques (UNIT 9)
Introduction
- You have studied about maps in your school text books and you know that mapping involves determining the geographic locations of features on the Earth. This is followed by transforming them into positions on a flat map using map projection.
- The idea of depicting the Earth on a flat map is easy to imagine and even simple to understand but the actual process of a map projection is really a complex task. The Earth is a complex three-dimensional object with physical dimensions, including height, width, depth, mass, and density.
- An important physical characteristic is its non-straight, curvilinear surface. This curvilinear property adds complexity to a map projection’s transformation of the Earth model or globe to a flat surface. Due to the Earth’s curvilinear surface, map projections always hold a degree of distortion.
Geodesy
- Geodesy, also known as geodetics, is the scientific discipline that deals with the measurement and representation of the Earth in geometrical and gravimetrical sense. Geodesy is defined as the science concerned with study of shape and size of the Earth.
- In geometric sense, it deals with the study of shape and size of Earth’s surface, the measurement of the position and motion of points on the surface. In gravimetric sense, it deals with the study of equipotential surfaces of the gravity potential. Every geodetic measurement is a function of gravity field which may vary from point to point. Unlike plane survey, geodetic survey involves complicated three-dimensional spherical geometry.
- There are two types of surveys i.e. plane survey and geodetic survey, that may be used in compiling large scale maps. Plane (or cadastral) survey, is commonly performed for a limited area. Thus, Earth’s curvature may not be taken into account because it is relatively insignificant over a small area.
- The lines of a plane survey are determined from ground observations, and are mapped as observed without being referred to as a spheroid. On the other hand, topographic maps are based on a framework developed by geodetic survey, and the ground observations are referred to as a spheroid as it involves a large area. Consequently, the two kinds of survey usually do not match.
- The study of geodesy began with mere curiosity and the never-ending human will to explain the Earth’s unknowns through logic. There exists the first remnant of geodetic analysis starting as far back as the early Greeks. Homer, Pythagoras, Plato, and others all had put efforts to describe the shape of the Earth. Homer (8th century B.C.), for instance, held the idea that Earth was a large flat disc, while Pythagoras (6th century B.C.), a mathematician, viewed Earth as a perfect sphere.
- Aristotle’s (4th century B.C.) arguments for a spherical Earth was more compelling as he noted that sailing ships always disappear into the horizon rather than becoming smaller dots. You will be interested to know that ancient Indians contributed significantly to geodesy. Indian mathematician Aryabhatta (476 to 550 A.D.) was the first person to determine the circumference of the Earth with a remarkable accuracy. The discovery that Earth rotates on its own axis from west to east is described in his famous book ‘Aryabhatiya’.
- Until about seventeenth century, the Earth was thought to be a perfect sphere. The change came around 1670, as a consequence of Newton’s theory of gravity. He proposed that earth’s shape slightly bulged out at the equator due to the greater centrifugal force generated by rotation. The equator bulging produces slight flattening at the poles.
Earth Models
- Earth’s rugged, irregular surface is difficult to be explained by mathematics for calculating the positions of Earth features. To effectively represent the shape and size of the Earth in scientific and real-life applications, a calculable, formula-driven model of the Earth is required. The closer a model comes to the actual surface of the Earth, the better it is for geographic positioning.
- Geoid (meaning earthlike) is an approximated figure of the Earth. In more technical terms, it is a sea level equipotential surface – the surface on which gravitational potential remains equivalent to its strength at mean sea level. However, it is not a smooth surface. The gravitational pull is not uniform throughout the Earth surface. This is mainly because of density variation inside the Earth. For example, gravitational pull of the Earth is stronger in areas rich with iron and other dense materials. This results in undulating geoid surface which is not smooth and regular.
- It is clear that Earth is not a perfect sphere, but rather slightly ellipsoidal in shape. For small scale mapping, shape of the Earth may be considered as spherical instead of ellipsoid. The spherical model of Earth is called Authalic Sphere, which may be defined as a sphere of the same surface area as that of ellipsoid. Cartographers use authalic sphere for mapping on a small scale, i.e., 1:1 million or smaller.
- Today’s precision GIS is built upon the advances in modern geodesy and the refreshed knowledge of the Earth’s true shape. With satellite imagery and modern physical science, it is evidently established that the Earth is a nearly spherical object that bulges in the middle and flattened at the poles. In this regard, ellipsoid can best represent an Earth as it poses a near resemblance to its shape without the inherent complexities.
Ellipsoid Models
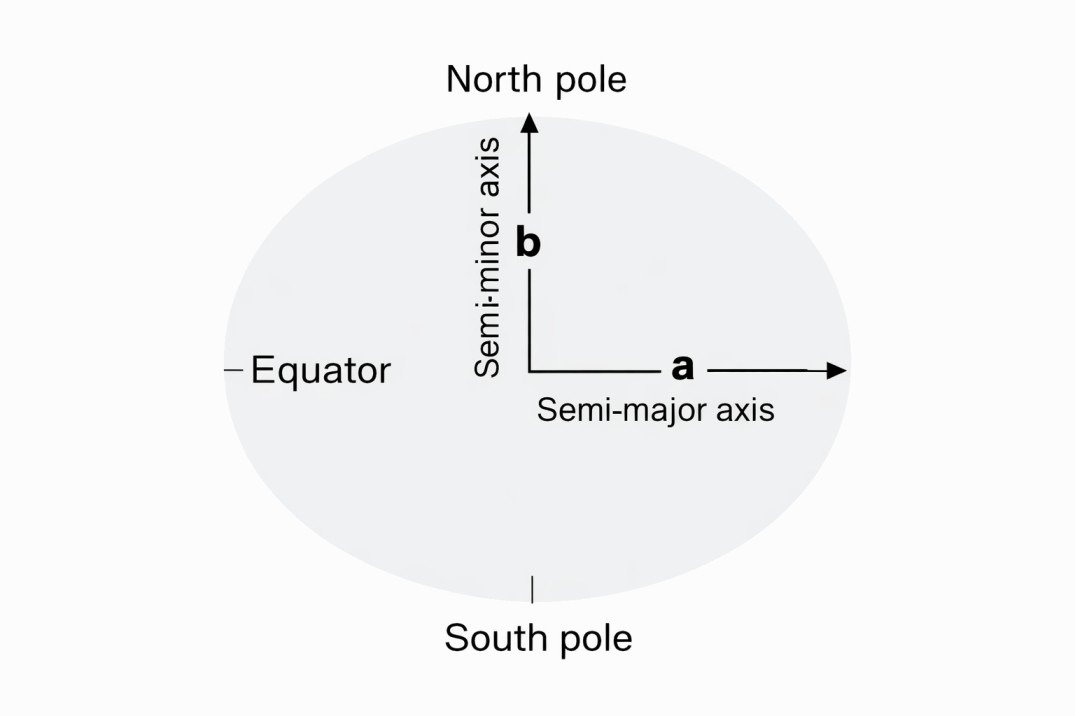
- You have read that Earth could be represented as ellipsoid. The Earth’s ellipsoid is an ellipse rotated upon its minor axis, which is functionally called the axis of rotation or axis of revolution. The purpose of a mathematical model is to simplify calculations. Since an ellipse is a two-dimensional shape and an ellipsoid is a more complex three-dimensional object, we utilise the figure of an ellipse to achieve this mathematical simplicity.
- Rotating this ellipse about the polar axis would outline a three dimensional model of the Earth called an oblate ellipsoid (also called oblate spheroid).
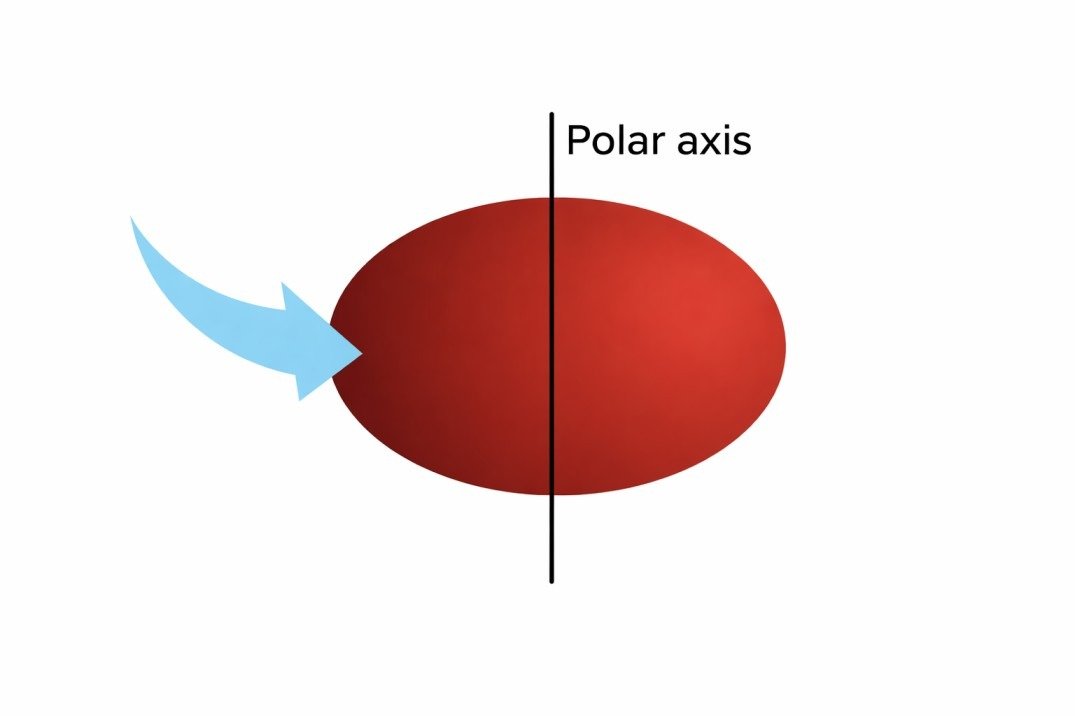
The ellipsoid’s flattening causes two unequal axes:
- a longer axis, and
- a shorter axis.
The north-to-south axis through the Earth’s core is the shorter axis and, as such, is called the minor axis or polar axis. The east-to-west axis through the Earth’s core is longer and is called the major axis or equatorial axis. In brief, the flattening of the ellipse is directly related to the differences in both the semi-major axis (half of the major axis) ‘a? and semi-minor axis (half of the minor axis) ‘b?. It is represented by the formula.
Flattening (f) = (a – b) / a
Earth’s flattening is sometimes displayed as a reciprocal called the inverse flattening. For instance, a flattening of 0.003389831 (or 1/295) can be portrayed as an inverse flattening of 295. The formula for inverse flattening is represented as:
Inverse Flattening (f -1) = 1 / f
= a / (a – b)
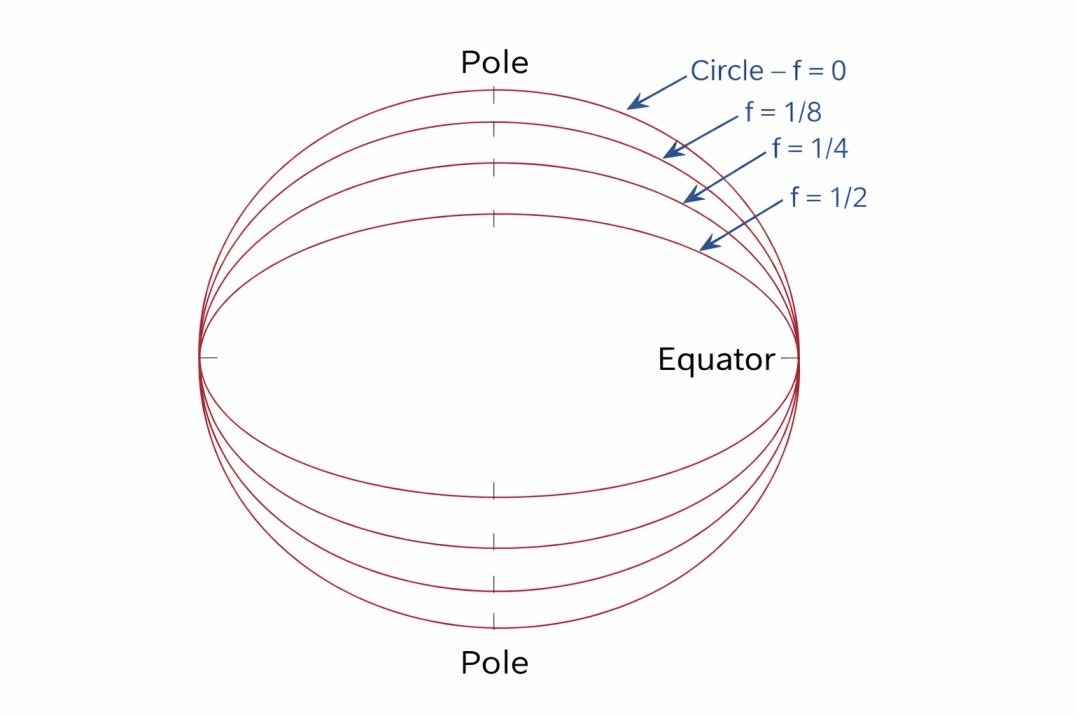
Below Fig. illustrates different flattening scenarios. However, in the case of the Earth, the polar axis measurement is only slightly shorter than the east-to-west equatorial axis measurement. Newton in the seventeenth century had predicted the flattening to be about 1/300th of the equatorial axis. And present day measurements show, it as 1/298th of the equatorial axis.
Use of Geoid, Sphere and Ellipsoid
- After reading the previous sections of this unit, you are now aware of the three approximations i.e. Geoid, Sphere and Ellipsoid are used to define Earth’s true shape in different ways. The geoid is considered as a reference from which elevations or heights can be measured.
- It is the reference surface for ground survey. The horizontal and vertical positions are mapped with reference to the geoid surface. Horizontal positions are later adjusted to the ellipsoid surface, because the irregularities on the geoid surface would make projection and other mathematical computations extremely complex. On the other hand, elevations are determined with reference to the geoid surface.
- The authalic sphere is the reference surface for small-scale maps of countries, continents and larger areas. This is because the difference between sphere and ellipsoid is negligible while mapping large areas on page size maps. There is also a significant increase in complexity of map projection equations for the ellipsoid than a sphere. In addition, the spherical and ellipsoidal equations for a particular map projection provide the same results for the small scale (1:1 million) maps.
- A sphere proves adequate along the equator (equatorial plane) but fails at locations closer to the poles. With large scale (1:10,000) maps, however, the difference between spherical and ellipsoidal approximations can be significant, and hence we need to take the Earth’s oblateness into account. The ellipsoid, also referred to as a spheroid, is a much better approximation for the shape of the Earth than the sphere; the poles are slightly flattened and the equator bulges. Unlike the sphere, the ellipsoid can handle dissimilar dimensions.
Which is the Best Reference Ellipsoid for You?
- Basically, every GIS and geographic information product is based upon a reference ellipsoid, which is defined as a standard ellipsoid with measured parameters. Over the years, numerous reference ellipsoids have been developed by various geodesists with measurements taken at different source points on Earth.
- From 1800 to till date, at least 20 determinations of Earth’s radii and flattening have been attempted from measurements taken widely at different locations. The foremost purpose of these various determinations is to develop a best fit model for specific part of the Earth compromising accuracy over other parts. Values for 10 different ellipsoids used as basis for mapping in various parts of the world are listed in Table…
| Name | Year | Semi-major axis ‘a’ (meters) | Semi-minor axis ‘b’ (meters) | Polar Flattening |
|---|---|---|---|---|
| Airy | 1830 | 6,377,563.40 | 6,356,256.91 | 1/299.32 |
| Everest | 1830 | 6,377,299.37 | 6,356,098.36 | 1/300.8 |
| Bessel | 1841 | 6,377,276.30 | 6,356,075.40 | 1/299.15 |
| Clarke | 1866 | 6,378,206.40 | 6,356,583.80 | 1/294.98 |
| Clarke | 1880 | 6,378,249.10 | 6,356,514.90 | 1/293.46 |
| International | 1924 | 6,378,388.00 | 6,356,911.90 | 1/297 |
| Krasovsky | 1940 | 6,378,245.00 | 6,356,863.00 | 1/298.3 |
| Australian | 1965 | 6,378,160.00 | 6,356,774.70 | 1/298.25 |
| WGS 72 | 1972 | 6,378,135.00 | 6,356,750.50 | 1/298.26 |
| WGS 84 | 1984 | 6,378,137.00 | 6,356,752.30 | 1/298.257 |
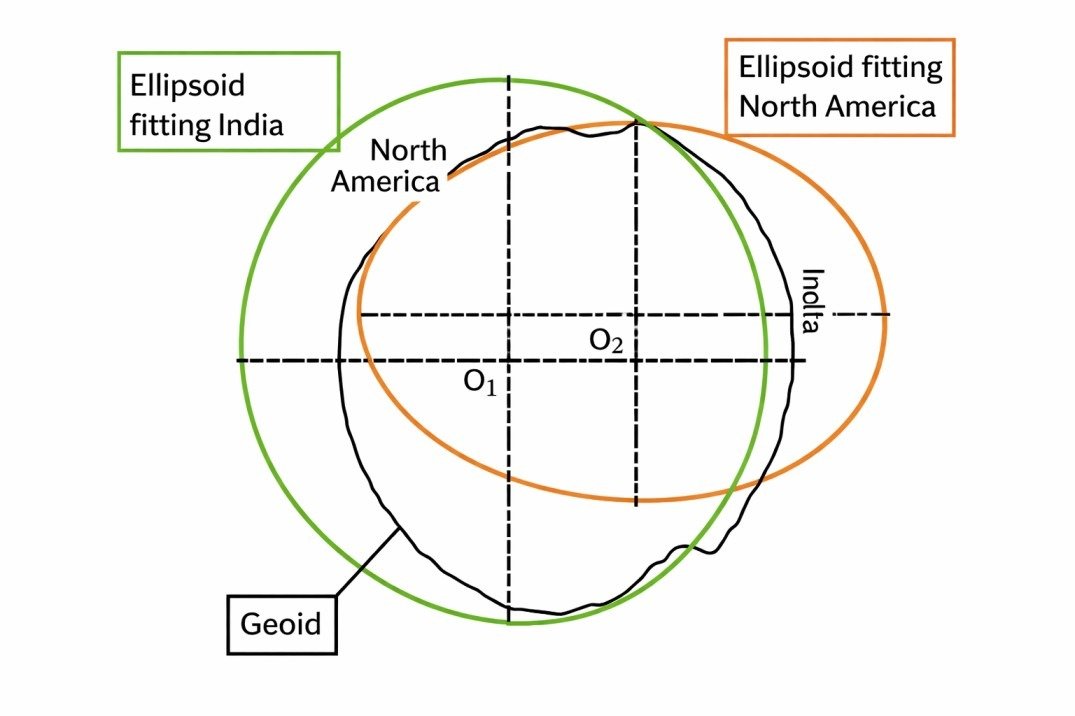
- These reference ellipsoids are only slightly dissimilar. Because of the differences in source data locations, certain reference ellipsoids work better than others for certain applications and for certain regions. For example, you should choose reference ellipsoid Everest 1830 for Asian GIS products because this ellipsoid is more suited for Asian region, whereas for other regions some other reference ellipsoid may be more suitable.
- Unlike Everest 1830 and other major area specific ellipsoids, WGS84 is more universal. As a result, it is one of the most widely used reference ellipsoids. It is determined from satellite orbital data and considered more accurate than the earlier ground measurement determinations. Although, it gives the best fit ellipsoid for the entire Earth, it may not offer best fit for a particular part of the Earth.